Summary

I submitted my project proposal for my Tetris AI.

I completed 3 more weeks of Machine Learning by Andrew Ng.

Project - Tetris AI

So fair for my project I’ve only done back round research on the area and studied machine learning.

For my project I submitted my project proposal which is just the overview of what my project is about and why I’m doing it and how I’m going to do.

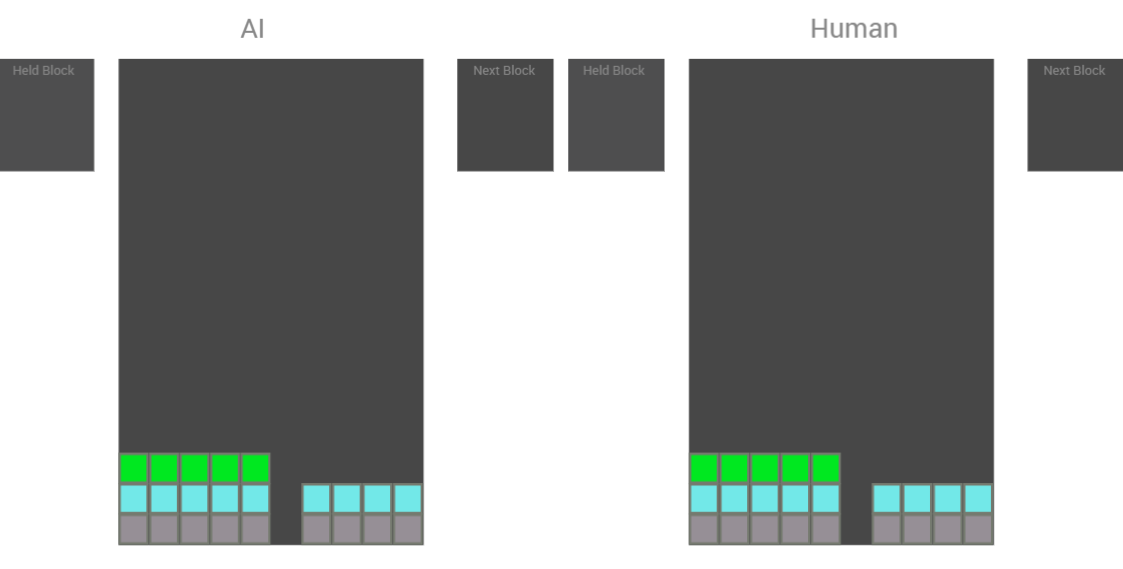
Below is one of the images for the layout of my Tetris game. Zero coding done yet and a long road ahead.

Tetris layout

Machine Learning - Coursea

Brief overview of what I learned in the week 3-5 of Machine Learning by Andrew Ng, and my answers for exercise 2.

What I learned -

Week 3

Multiclass classification one vs all

Which is how to work with problems that have more than 2 classifications for a case were maybe you are trying to decide if and object is a cat dog or person. Rather than regular classification were you want to see if something is true or not.

Overfitting

Overfitting can occur when the algorithm you are using matches the training data extremely well but isn’t suitable for data outside of it.

Regularisation

Is a way of shrinking the coefficient estimates as to try avoid overfitting.

Week 4

Model Representation of a neural network

How neural networks look and work.

Forward propagation

The step by step calculation of the network from the inputs to the outputs.

Week 5

Backpropagation

A way of evaluating the expression for the derivative of the cost function. It tells us how quickly the cost changes when we change the weights and biases.

Gradient Checking

A way to check if your gradient is correct and to help confirm your algorithm is working properly.

Python solutions for Exercise 2

Sigmoid Function

    g = 1 / (1 + np.exp(1)**(-z))

Logistic Regression Cost & Gradient

    h = sigmoid(theta.dot(X.T))
    J = (1/m)*np.sum(np.dot(-y,np.log(h)) - np.dot((1-y),np.log(1-h)))
    grad = (1/m)*(np.dot((h - y),X))

Predict

    p = np.round(sigmoid(np.dot(X,theta)))

Regularized Logistic Regression Cost & Gradient

    s = np.ones(theta.shape)
    s[0] = 0
    h = sigmoid(theta.dot(X.T))
    J = (1/m)*np.sum(np.dot(-y,np.log(h)) - np.dot((1-y),np.log(1-h))) + ((lambda_/(2*m))*np.sum(np.square(theta[1:])))
    grad = (1/m)*(np.dot((h - y),X)) + (lambda_/m)*theta 
    grad[0] = grad[0] - ((lambda_/m)*theta)[0]

Useful resources

My github for these exercises

3Blue1Brown on youtube guy who goes over the maths of these topics really well and in a very visual way.

github repo by some nice people who converted the assignments into Python, so you can submit them as python!

Road Ahead -

Over the next week I plan to:

Thanks for reading and happy coding!